Gang's Blog.
Gang's Blog.

机器学习算法-K近邻

Gang Gang 收录于 机器学习
 约 800 字 预计阅读 4 分钟 

机器学习相关算法

  1. K-近邻
  2. 线性回归
  3. 线性回归的改进-岭回归
  4. 逻辑回归（分类）
  5. 决策树
  6. 朴素贝叶斯
  7. SVM
  8. EM算法
  9. HMM模型
  10. K-MEANS
  11. 集成学习

K-近邻(KNN)算法

概念

简单理解：根据最靠近自己的人的类别，判断自己的类别。

K Nearlest Neighbor 算法又叫做KNN算法，这个算法是机器学习里面一个经典和比较容易理解的算法。

定义

如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于一个类别，则该样本也属于这个类别。

实现过程

有如下数据，需要预测《唐人街探案》属于那种电影类型。

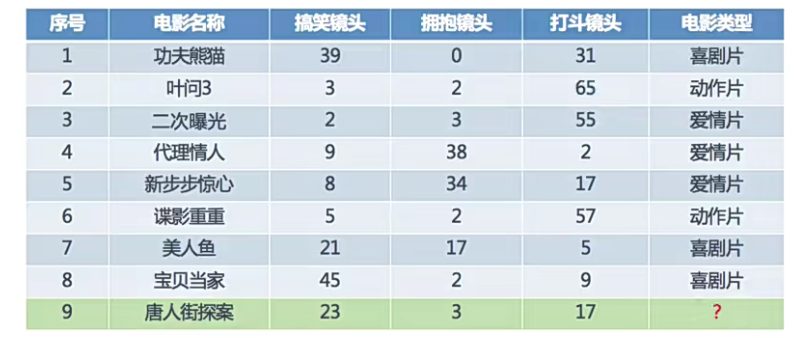
image-20230205200340501

从图中可以看出部分规律：

  • 喜剧片：搞笑镜头多

  • 动作片：打斗镜头多

  • 爱情片：拥抱镜头多

使用K-近邻来分析：

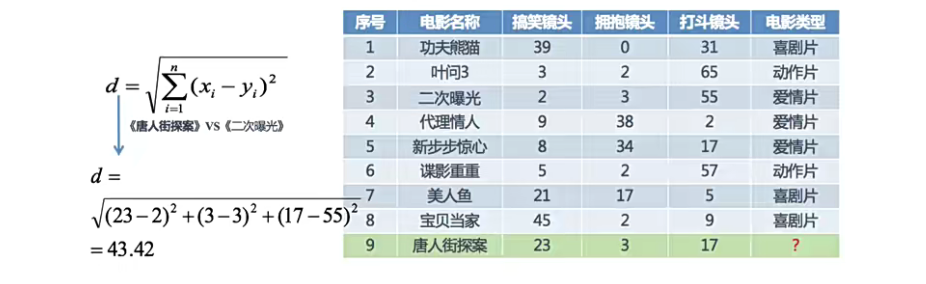
image-20230205200709529

分别计算每个电影和被预测电影的距离：

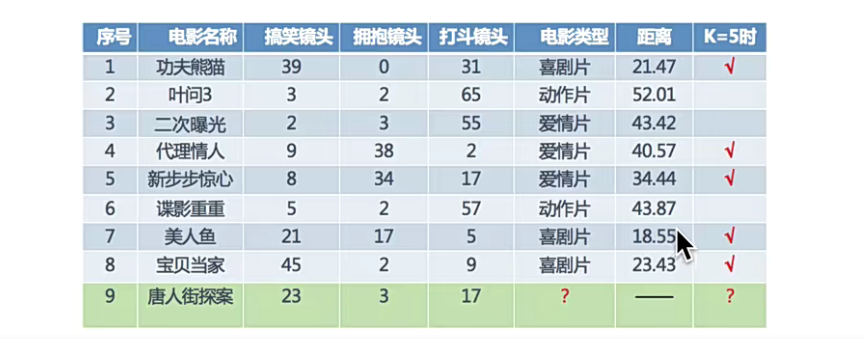
image-20230205200751179

从图中的距离可以判断出《唐人街探案》也属于喜剧片(18.55最近)

距离度量方式

欧式距离（Euclidean Distance）

两个样本之间的距离公式可以通过如下公式计算，又叫欧式距离

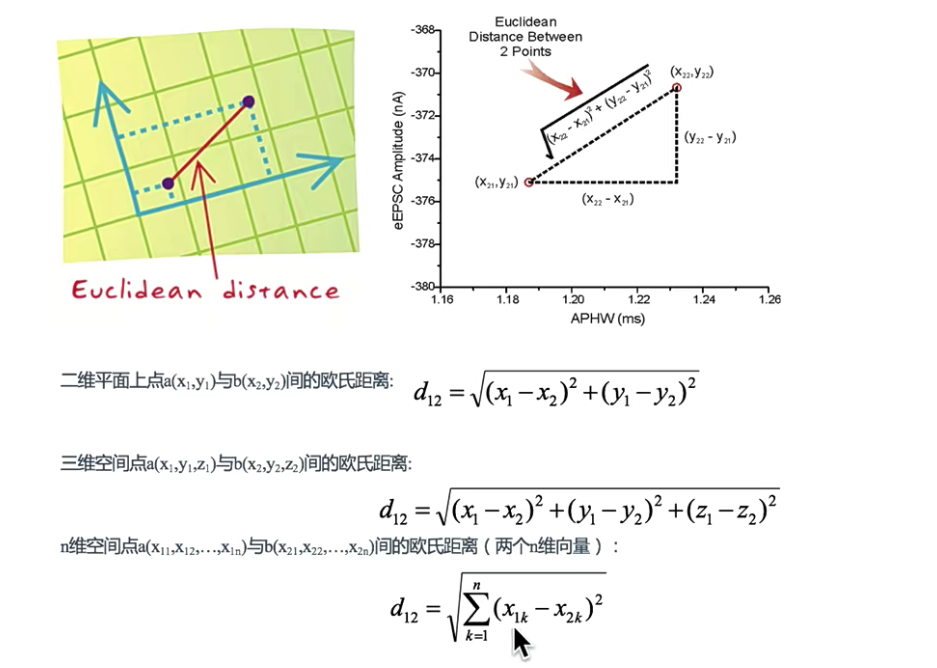
image-20230205200011371

曼哈顿距离（Manhattan Distance）

在曼哈顿街区从一个十字路口开车到另外一个十字路口，驾驶的距离显然不是直线距离，这个驾驶距离就是曼哈顿距离，曼哈顿距离也称为是城市街区距离。

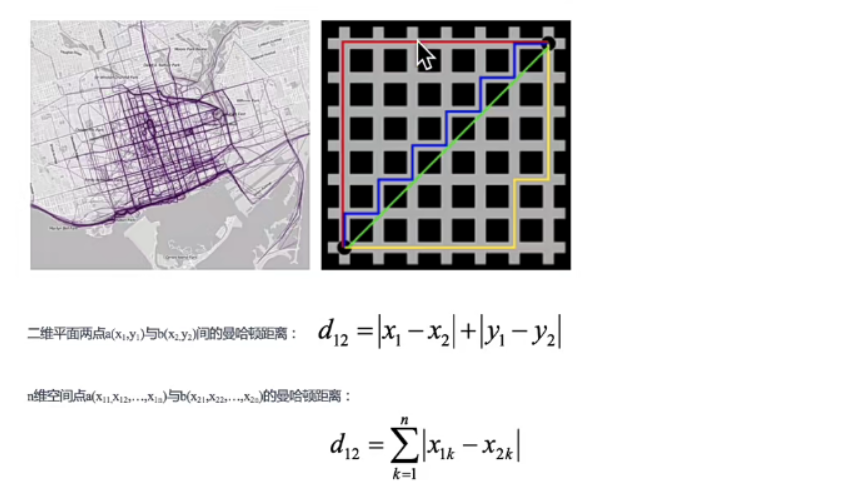
image-20230219104854695

切比雪夫距离

国际象棋中，国王可以直行，横行，斜行。所以国王走一步可以移动到相邻8个方格中的任意一个（斜着走也算1），国王从格子(x1, y1)走到格子(x2, y2)最少需要多少步这个距离就叫做切比雪夫距离

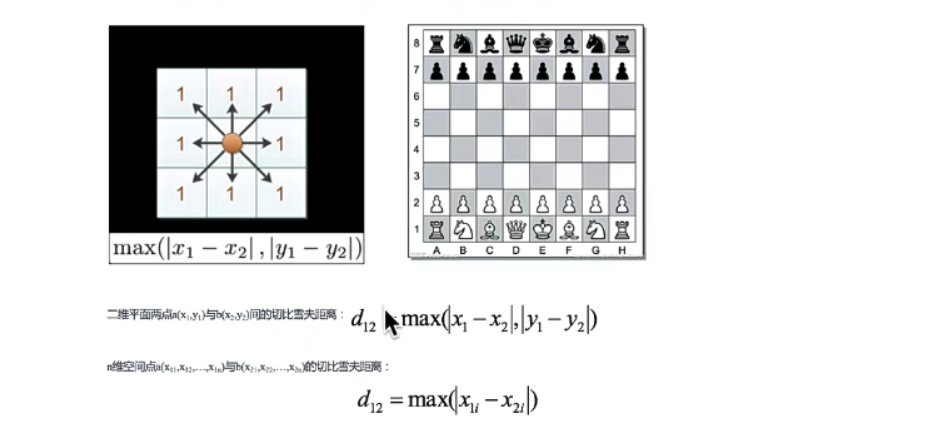
image-20230219105309995

闵可夫斯基距离

image-20230219105757073

流程总结

  1. 计算已知类别数据集中的点与当前点之间的距离
  2. 按距离递增次序
  3. 选取与当前点距离最小的K个点
  4. 统计前K个点所在的类别出现的概率
  5. 返回前K个点出现频率最高的类别作为当前点的预测分类

API的使用

Scikit-learn

包含内容：

  • Classification（分类）

  • Regression（回归）

  • Clustering（聚类）

  • Dimensionally reduction（降维）

  • Model Selection（模型选择）

  • Preprocessing（预处理）

1
2
3
4
5
6

# 安装
pip install scikit-learn==0.19.1


# n_neighbors: int 默认为5。查询默认使用的邻居数
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)

例子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import sklearn
from sklearn.neighbors import KNeighborsClassifier

# 构造数据
x = [[0],[1],[2],[3]]
y = [0,0,1,1]

# 训练模型
# 实例化一个估计器对象
estimator = KNeighborsClassifier(n_neighbors=2)

# 调用fit方法进行训练
# 可以这样理解，x是特征值
estimator.fit(x, y)

# 数据预测
estimator.predict([[1]])

超参数K值的取值范围对算法的影响

  • k值选择过小：容易收到异常点的影响
  • k值选择过大：受到样本均衡问题的影响

在李航博士的《统计学习方法》上所说：

  2. 选择较小的K值，就相当于用较小的领域中的实例进行预测，“学习”近似误差会减小，只有与输入实例较进或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大，换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合。

  3. 选择较大的K值，就相当于用较大的领域中的实例进行预测，其优点是可以减少“学习”的估计误差，但缺点是学习的近似误差会增大，这时候，与输入实例较远（不相似的）训练实例也会对预测器起作用，使预测发生错误，且K值的增大就意味着整体的模型变的简单。

  4. K=N（n为训练样本个数）则完全不足取，应为此时无论输入的实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单，忽略了训练实例中大量的有用的信息。

在实际运用中，K一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组训练集和验证集）来选择最优的K值

近似误差：

  • 对现有训练集的训练误差，关注训练集
  • 如果近似误差过小，可能会出现过拟合的情况，对现有的训练集能有很好的预测，但是对未知的测试样本，将会出现较大偏差的预测
  • 模型本身不是最接近最佳模型

估计误差：

  • 可以理解为对训练集的测试误差，关注测试机
  • 估计误差较小说明对未知数据的预测能力好
  • 模型本身最接近最佳模型

KD-Tree的构建和搜索实现过程

为什么需要KD-树？

因为KNN算法最简单的实现方法是线性扫描（穷举搜索），即计算输入实例与每一个训练实例的距离，计算并存储好之后，在查找K近邻，当训练集很大的时候，计算非常耗时。

为了提高KNN的搜索效率，可以考虑使用特殊的结构存储，以减少计算距离的次数

原理

为了避免每次重新计算一遍距离，算法会将距离信息保存在一棵树里，这样在之前的树里的查询距离信息，尽量避免重新计算，其基本原理是：如果A和B的距离较远，B和C的距离很近，则A和C的距离也很远。在这个时候就可以在合适的

时候跳过距离较远的点。这样优化后的算法复杂度可以降到O(DNlog(N))

另外一种算法称为Ball Tree

构造

  1. 维度划分
  2. 计算中位数
  3. 划分左右子树
  4. 划分剩余维度，重复2,3
  5. 所有的维度都划分一遍直到所有的点都挂在树上

案例

给定一个二维数据集T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造一个平衡KD树

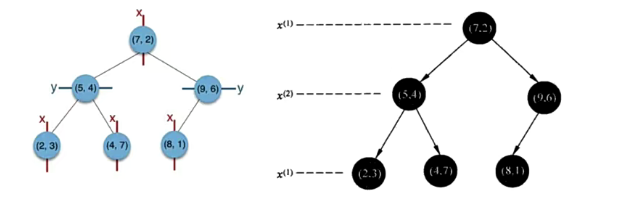
image-20230225174930183

  1. 维度划分：

    • 第一维度-（x轴）：2,5,9,4,8,7 排序之后：2,4,5,7,8,9

    • 第二维度（y轴）：3,4,6,7,1,2 排序之后：1,2,3,4,6,7

      计算两个维度的方差，选择方差较大的维度进行划分，这里选择x轴进行划分

  2. 计算划分维度的中位数，选择距离中位数最近点作为分割点，如果两个点距离中位数的距离相等就随机选择一个，这个点就是当前树的根节点

  3. 在这个维度上小于这个分割点的为左子树，大于这个分割点的为右子树

  4. 在剩下的维度上选择一个方差最大的维度进行划分，重复2,3,

  5. 所有维度划分一遍，直到所有的点都挂在树上

查找

案例

鸢尾花种类预测

Scikit-learn中数据集API介绍

  • sklearn.datasets
    • 加载获取流行的数据集
    • datasets.load_*()：获取小规模的数据集
    • datasets.fetch_*(data_home=None)：获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录，默认是~/scikit_learn_data/

skleanrn小数据集

  • sklearn.datasets.load_iris()

    加载并返回鸢尾花数据集

1
2
3
4
5
6

from sklearn.datasets import load_iris
from sklearn.datasets import fetch_20newsgroups

# 获取小数据集
iris = load_iris()
print(iris)

sklearn获取大数据集

  • sklearn.datasets.fetch_20newsgroups(data_home, subset='train')
    • subset：’“train"或者’test’或者"all"可选，选择要加载的数据集
    • 训练集的“训练”，测试机的“测试”，两者的“全部”
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

from sklearn.datasets import load_iris
from sklearn.datasets import fetch_20newsgroups

# 获取小数据集
# iris = load_iris()
# print(iris)

# 获取大数据集
news = fetch_20newsgroups()
print(news)

修复fetch_20newsgroups下载缓慢问题

  1. 从http://qwone.com/~jason/20Newsgroups/上面找到Data然后再找到20news-bydate.tar.gz ，然后下载

  2. 将下载好的压缩包放到C:\Users\用户名\scikit_learn_data\20news_home这个目录下

​ image-20230508224141929

  1. 打开下面这个文件(_twenty_newsgroups.py)，可以看出红框标记的部分是下载数据集的部分代码，也就是上面tar包的下载地址

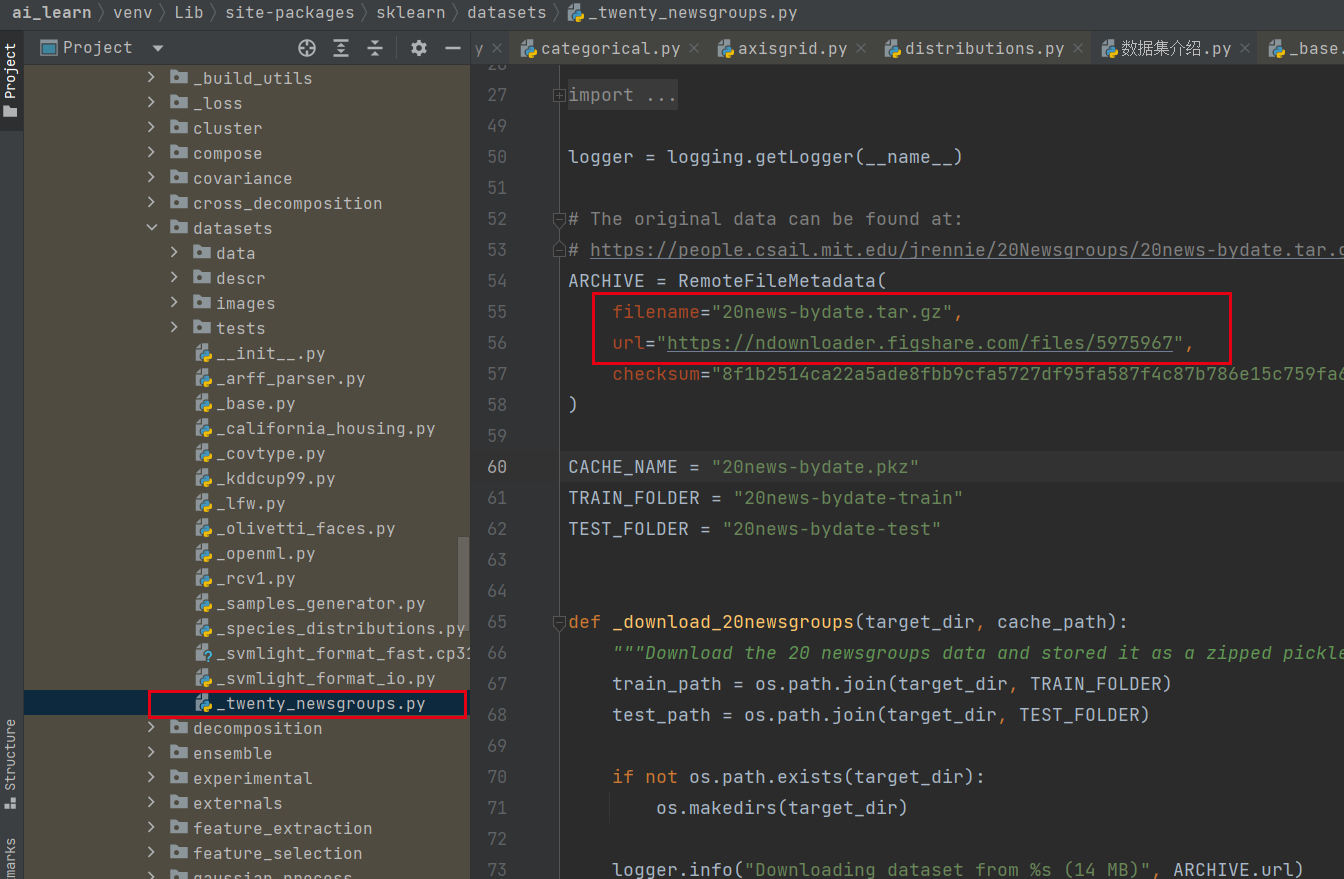
    image-20230508224555313

    在_download_20newsgroups这个方法中按照下图方式修改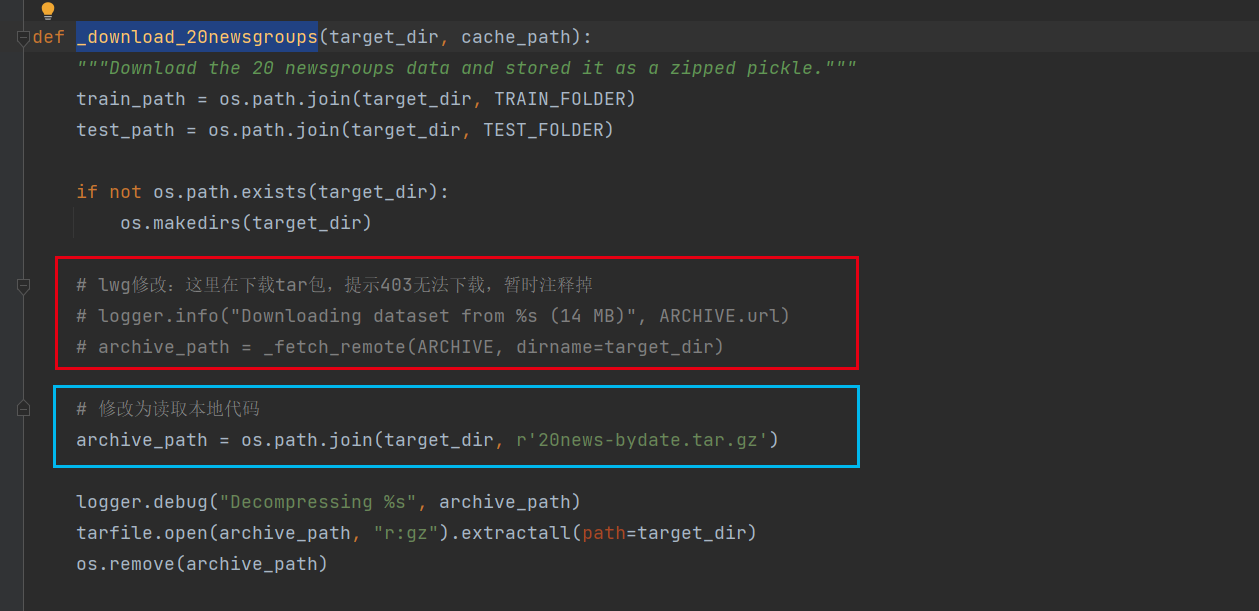

    image-20230508225249197

    最终代码如下

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

    def _download_20newsgroups(target_dir, cache_path):
    """Download the 20 newsgroups data and stored it as a zipped pickle."""
    train_path = os.path.join(target_dir, TRAIN_FOLDER)
    test_path = os.path.join(target_dir, TEST_FOLDER)

    if not os.path.exists(target_dir):
        os.makedirs(target_dir)

    # lwg修改：这里在下载tar包，提示403无法下载，暂时注释掉
    # logger.info("Downloading dataset from %s (14 MB)", ARCHIVE.url)
    # archive_path = _fetch_remote(ARCHIVE, dirname=target_dir)

    # 修改为读取本地代码
    archive_path = os.path.join(target_dir, r'20news-bydate.tar.gz')

    logger.debug("Decompressing %s", archive_path)
    tarfile.open(archive_path, "r:gz").extractall(path=target_dir)
    os.remove(archive_path)

    再次执行fetch_20newsgroups()方法后可以看到tar包已经被解压

    image-20230508225637568

    ​

​

Sklearn数据集返回值介绍

  • load和fetch返回中的数据类型datasets.base.Bunch(字典格式)

    • data：特征值
    • target：标签数组
    • DESCR：数据描述
    • feature_names：特征名，
    • target_names：标签名
     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

    print("数据集的特征值: \n", iris.data)
print("数据集的目标值: \n", iris.target)
print("数据集的描述: \n", iris.DESCR)
print("数据集的特征名: \n", iris.feature_names)
print("数据集的目标名: \n", iris.target_names)


数据集的特征值: 
 [[5.1 3.5 1.4 0.2]
 [4.9 3.  1.4 0.2]
 [4.7 3.2 1.3 0.2]
 [4.6 3.1 1.5 0.2]
 ......
 ]

数据集的目标值: 
 [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]
数据集的描述: 
 .. _iris_dataset:

Iris plants dataset
--------------------

**Data Set Characteristics:**

    :Number of Instances: 150 (50 in each of three classes)
......

数据集的特征名: 
 ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
数据集的目标名: 
 ['setosa' 'versicolor' 'virginica']

数据可视化 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.datasets import fetch_20newsgroups

# 获取小数据集
iris = load_iris()

iris_d = pd.DataFrame(data=iris.data, columns=["Sepal_Length", "Sepal_Width", "Petal_Length", "Petal_Width"])
iris_d["target"] = iris.target

print(iris_d)


def iris_plot(data, col1, col2):
    sns.lmplot(x=col1, y=col2, data=data)
    plt.show()


iris_plot(iris_d, "Sepal_Width", "Petal_Length")

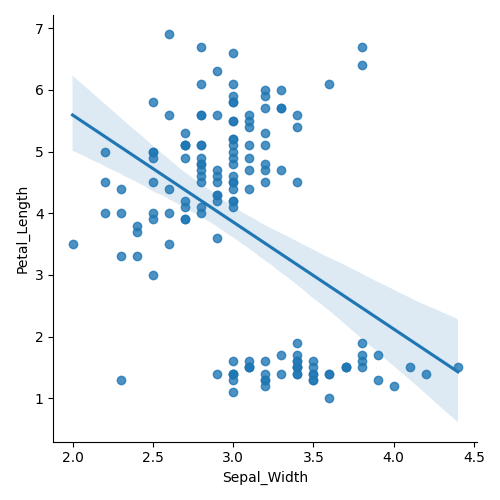
image-20230517222337393

添加hue和target参数 

1
2
3

def iris_plot(data, col1, col2):
    sns.lmplot(x=col1, y=col2, data=data, hue="target", fit_reg=False)
    plt.show()

在iris_plot函数中，hue和fit_reg是seaborn包中的lmplot函数的额外参数。

  1. hue：hue参数允许您指定数据集（data）中的一个变量，用于为散点图中的数据点着色。在这个例子中，"target"列被用作hue参数。"target"列中的每个唯一值将被分配不同的颜色，这样可以更容易地区分图中的不同类别或组。

  2. fit_reg：fit_reg参数是一个布尔标志，用于控制是否对散点图进行回归拟合并显示回归线。当设置为False，就像在给定的代码中一样，不会绘制回归线。如果设置为True，将对数据点进行回归拟合，并在图中显示回归线，显示变量之间的总体趋势或关系。

因此，通过设置hue="target"，散点图中的不同值将具有不同的颜色，有助于可视化不同的类别。而通过设置fit_reg=False，图中不会显示回归线。

数据集的划分

机器学习一般的数据集会划分为两个部分

  • 训练数据：用于训练，构建模型
  • 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

  • 训练集：70% 80% 75%
  • 测试集：30% 20% 25%

数据集划分API

  • sklearn.model_selection.train_test_split(arrays, *options)

    • 参数：
      • x数据集的特征值
      • y数据集的标签值
      • test_size测试集的大小，一般为float
      • random_state随机数种子，不同的种子会造成不同的采集结果，相同的种子采集结果相同
    • return：
      • x_train， x_test，y_train，y_test
    1
2
3
4
5

    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)
print("训练集的特征值: \n", x_train)
print("训练集的目标值: \n", y_train)
print("测试集的特征值: \n", x_test)
print("测试集的目标值: \n", y_test)

使用KNeighborsClassifier实现分类

较差验证的概念极其作用

相关内容

更新于 2023-02-05 
CC BY-NC-SA 4.0
机器学习算法K-近邻
返回 | 主页
0%