Gang 收录于人工智能

2024-08-21 约 300 字预计阅读 1 分钟

多元线性回归

回归问题主要关注确定一个唯一的因变量（需要预测的值y）和一个或多个数值型的自变量（预测变量x）之间的关系。

简单线性回归

对应的公式如下： $y = a+bx$

$y$：是目标变量，即未来要预测的值

$x$：是影响$y$的因素，

$a$，$b$：是要求的模型

将已知的x带入公式，并将估算出来的a、b带入公式，计算后得到的y‘之间的误差，最优解即最小误差的那组a和b。

整体的误差通常称为Loss，Loss可以通过损失函数Loss function得到。

回归简单的来说就是“回归平均值（Regress to the mean）”，并不是把历史数据当成未来的预测值，而是会把期望当最预测值。

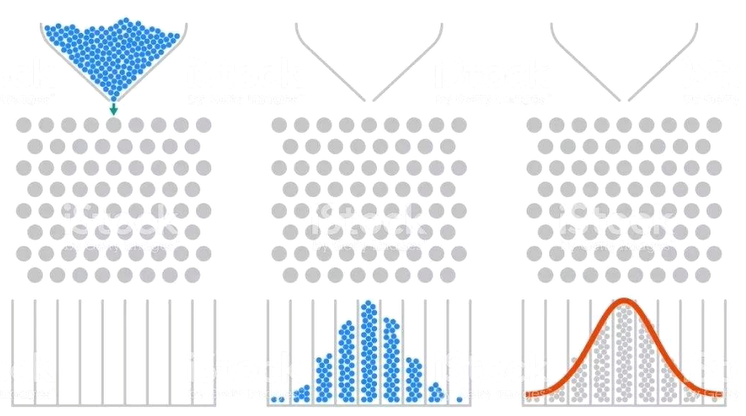
中心极限定理（Central limit theorem）是概率论中讨论随机变量序列部分和分部渐进于正态分布的一类定理。这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量累积分布函数逐点收敛到正态分布的积累分布函数的条件。

最大似然估计（Maximum Likelihood Estimation，MLE）是一种在统计学和机器学习中广泛应用的方法，用于估计模型参数，使得在给定数据下模型的概率（或似然函数）最大化。简单来说，最大似然估计是通过找到使观测数据最有可能发生的参数值。

假设你有一组独立同分布的观测数据 $(X = {x_1, x_2, \dots, x_n} ) $，这些数据来自某个概率分布，其概率密度函数由 $ f(x|\theta) $ 给出，其中 $ \theta $ 是我们需要估计的参数。

步骤：

定义似然函数：似然函数表示在给定参数 $ \theta $ 下，观测数据 $ X $ 出现的概率。对独立同分布的数据集，似然函数可以表示为所有数据点的联合概率：

$ L(\theta) = f(x_1|\theta) \cdot f(x_2|\theta) \cdot \ldots \cdot f(x_n|\theta) = \prod_{i=1}^{n} f(x_i|\theta) $
取对数：通常，我们会对似然函数取对数以简化计算。这被称为对数似然函数：

$ \ell(\theta) = \log L(\theta) = \sum_{i=1}^{n} \log f(x_i|\theta) $

取对数的原因是对数函数是单调递增的，且能够将乘法转化为加法，简化微分操作。
最大化对数似然函数：

最大似然估计的目标是找到参数 $\theta $ 使得对数似然函数 $ \ell(\theta) $ 最大化。即，求解以下问题：

$ \hat{\theta}_ {MLE} = \arg\max_{\theta} \ell(\theta) $

通常，这一步通过求解对参数 $ \theta $ 的对数似然函数的导数并设为零来完成：

$ \frac{\partial \ell(\theta)}{\partial \theta} = 0 $

解这个方程可以得到参数 $ \theta $ 的估计值 $ \hat{\theta}_{MLE} $。

例子：正态分布的参数估计

假设你有一组数据 $ X = {x_1, x_2, \dots, x_n} $ ，并且你认为这些数据来自一个正态分布 $ N(\mu, \sigma^2) $ 。那么正态分布的概率密度函数为：

$ f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) $

似然函数：

$ L(\mu, \sigma^2) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x_i - \mu)^2}{2\sigma^2}\right) $
对数似然函数：

$ \ell(\mu, \sigma^2) = \sum_{i=1}^{n} \left( -\frac{1}{2}\log(2\pi\sigma^2) - \frac{(x_i - \mu)^2}{2\sigma^2} \right) $
最大化对数似然函数：

通过对$ \mu $ 和 $ \sigma^2 $ 求偏导数并设为零，可以得到:

$\hat{\mu}_ {MLE} = \frac{1}{n} \sum_{i=1}^{n} x_i$

$ \hat{\sigma}^2_{MLE} = \frac{1}{n} \sum_{i=1}^{n} (x_i - \hat{\mu})^2 $

这两个公式表明，在正态分布假设下，样本均值是均值参数 $ \mu $ 的最大似然估计，而样本方差是方差参数 $ \sigma^2 $ 的最大似然估计。

优点：

缺点：